Learning a Quadcopter Flip with Reinforcement Learning

Usually for a controls problem such as a quadcopter flip, there are two controllers involved. The first is an energy controller which adds energy to the system. This causes the quadcopter to throw itself into the air to initiate the flip. As the quadcopter comes around, the second controller, a stabilizing controller, comes into play and returns the drone to its original position.

In this project, my partner Jialun Bao and I attempt to use neural networks to develop an end-to-end control law to govern the quadcopter flip. What we ended with was a neural controller as an energy gain controller to initiate the flip, and then a classical stabilizing PI controller as the stabilizing controller. This hybrid controller allowed for a 2D simulated model of a quadcopter to successfully flip.

3D Simulation

This 3D simulation was built by Abhijit Majumdar. The 3D quadcopters have 6 total states, 3 positional states for the x, y, and z positions, and 3 orienting states, which are the Euler angles of the model. We note that a quarternion model may provide a better system when defining the reward structure of the quadcopter.

The quadcopter is controlled by four thrust vectors at the ends of each of the arms which correspond to each rotor. Our control system relies on controlling the thrust from the rotors. We assume an internal controller is used to further convert our desired control action into the proper motor voltages, but is not considered in our design.

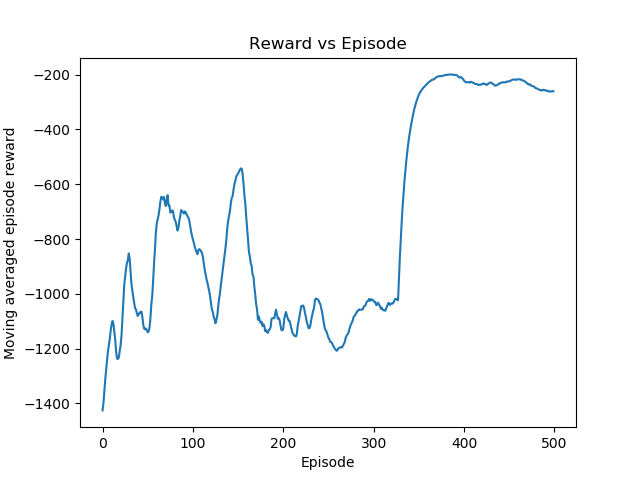
We define our reward as a positive fixed amount per instant the simulation is within some predefined stable bounds, with a penalty based on the euclidean distance the state vector is from the target state vector. With this system, we achieve attitude (orientation) control of the quadcopter, however, we notice positional drift.

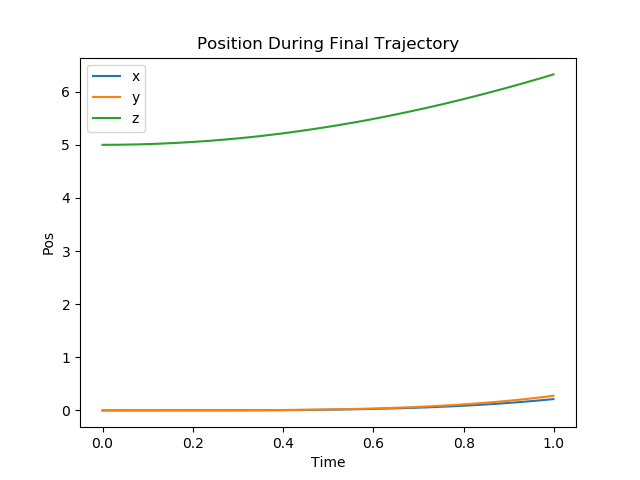We continued to test with different reward structures but none of them managed to create a working stabilizing controller to form the basis of our flip. We decided to tackle a simplified 2D version of the problem.

2D Simulation

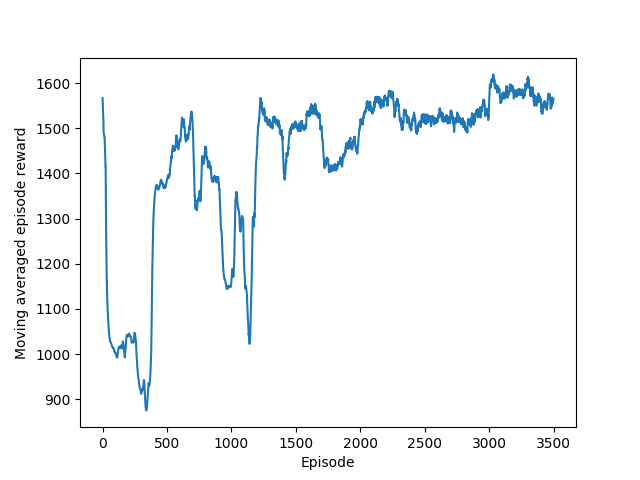
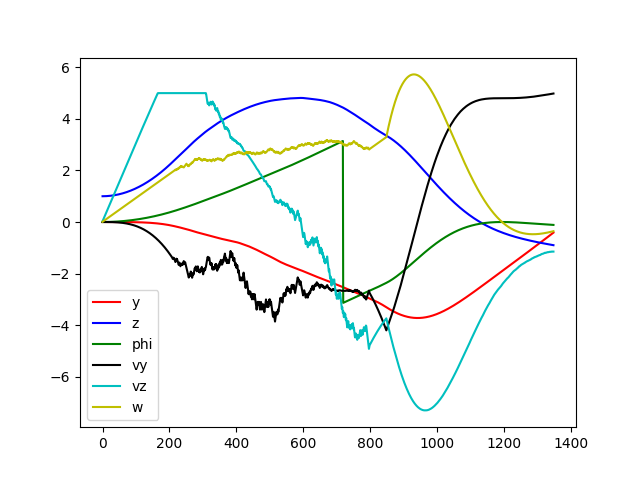
We built the 2D simulation based on first principles and used a similar code base to the 3D simulator. This 2D form has 2 positional states, a y and z axis, and 2 rotational components for a total of 4 states. We initially tried to use the neural network to learn a stabilizing controller, but we ran into similar problems as with the 3D case. Therefore, we chose to learn an energy controller instead and implemented a PI controller as the stabilizing controller. The end result was a network that was capable of performing the flip. We see most states as well as the derivatives to those states approaching zero near the end of the maneuver.

Proximal Policy Optimization (PPO)

The reinforcement learning algorithm we tried to use was Proximal Policy Optimization (PPO), an improvement over Trust-Region Policy Optimization (TRPO). We chose an onboard gradient-based method, because we had continuous action states. Like all RL algorithms, we aim to maximize the expected discounted rewards. More details on TRPO and PPO.

Blooper Reel

The fun part about reinforcement learning is that you don’t really know what the algorithm will do and where it will end up. Every so often we would visually sample the network and evaluate the performance. This led to some interesting results.

References

1. Trust Region Policy Optimization - Schulman, Levine, et al. (2015)
2. Proximal Policy Optimization Algorithms - Schulman, Wolski, et al. (2017)
3. R. Beard, Quadrotor Dynamics and Control, 2008.
4. V. Kumar, “2-d quadrotor control” (Lecture)
5. P. H. et al, “Deep reinforcement learning that matters,” 2017.