Thesis

Controls is an interesting field. It’s what keeps our airplanes in the air, and what keeps our homes at the perfect temperature. It’s how farmers keep grain at the right humidity, and how SpaceX lands their Falcon-9s. The hard part about controls is modeling how the system normally behaves, because that’s really one of the most important components of any feedback controller.

You can imagine trying to model the dynamics of a system is pretty difficult, and approximations have to be made all of the time to simplify even what seem to be easy problems. Even a pendulum, a simple ball on a stick, exhibits enough nonlinear behavior that approximations must be made to create these working models.

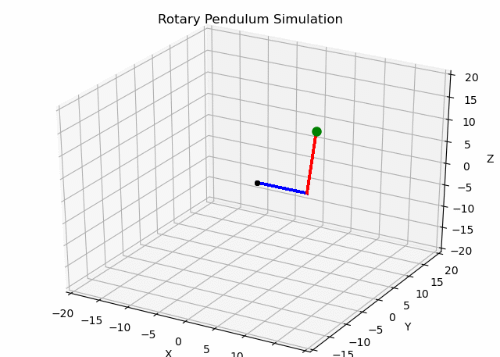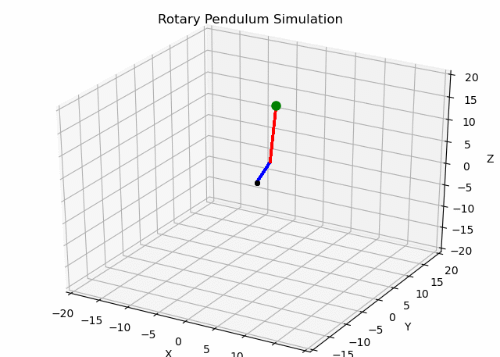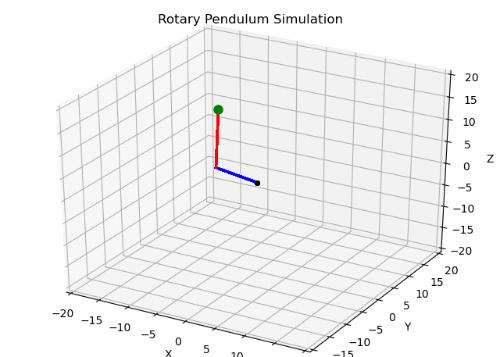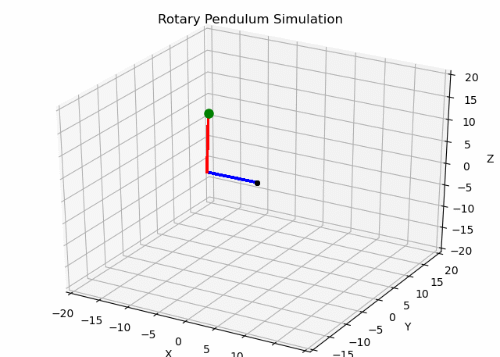
Building detailed models based on the physics of a system is hard. Fortunately, getting data on the system dynamics is easier. We look to using machine learning to model a mechanical system’s behavior. As an extension, we use machine learning to learn a control law that stabilizes a rotary pendulum. We choose this because it’s a 3-dimensional problem with two nonlinear frames, a rotary arm and a pendulum arm.

.

The following is a brief overview of the objectives of my thesis. Please refer to it for more details.

Static models

We first learn a direct static model of a mechanical system using a neural network. We choose to work with the same framework as this paper that introduces differentiable programming (delP) with a trebuchet. We wanted to apply this to the systems that we’re working with, so we chose to tackle this problem in Python.

The issue with learning mechanical systems is that the outputs to the neural network are control law outputs. They tell some actuator to the system how to behave. The result of that actuation is a change in the dynamics, and therefore a change in the states to the system. However, loss functions make the most sense when we try to regulate the states of the system to a desired state. We allow the control law to fluctuate and be whatever is needed to reach the desired state.

The issue is now that our desired loss functions are no longer differentiable in the outputs of our neural network, because we need to pass our inputs through an ODE-solver. Connecting the two and allowing for gradients to be propagated back through the ODE solution step back into the neural network is the goal of differentiable programming. We chose to use a finite difference estimation to solve for the gradient at the output which is then fed back into the neural network through backpropagation.

We learned the dynamics of the trebuchet as well as a control law directly and are able to reach specific targets with an mean absolute error of ~1.22%. By changing the environmental states such as wind speed and target distance, we can determine the optimal control law needed to reach that target.

Dynamic models

When it comes to dynamic models such as the rotary pendulum, we tried learning the control law directly. The issue there is that defining a good loss function that clearly outlined the desired dynamic behavior was difficult. Simply trying to zero-out the states caused the network to overshoot, because the optimal step found through gradient descent was to quickly return to the equilibrium position. However, there’s no sense of temporal tracking for the next states as would be found in a traditional feedback controller.

This concept of tracing a “path” through the state-space is what led us to use reinforcement learning as a method to learn the control law for a dynamic model. We chose a Deep Q-Network as a baseline RL model. As DQNs require discrete action spaces, we discretized our pendulum’s control action, the torque to the pendulum arm, and learned a stabilizing model.

The result was actually an interesting behavior in which the model was stable while moving at a constant angular velocity. Further improvements to the reward function could improve performance such that the rotary pendulum stabilizes and zeros all states.